Practice Problems
Q-1) Find the number of 2 digit positive integers that are divisible by both of their digits.
Q-2) How many ways are there to arrange the numbers 1,2,3…,64 on a 8×8 chessboard such that the numbers in each row and in each column are in A.P.?
Q-3) 5 points are situated on the plane in such a way that no 2 of the straight lines joining them are parallel, perpendicular or coincident. From each point, perpendiculars are drawn to all the lines joining the other 4 points. Determine the maximum number of intersections that these perpendiculars can have.
Q-4) Let m,n,k be positive integers with \(k\le \text{min}(m,n)\). How many ways are there to place \(k\) rooks on an \(m\times n\) chessboard such that none of the rooks attack each other?
Q-5) Consider an equilateral triangle of \(n\), we tile the triangle and create \(n^2\) equilateral triangles of side length 1 as shown below.
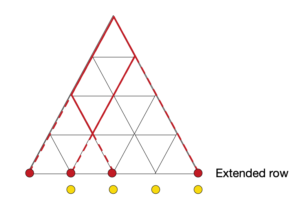
Find the number of parallelograms formed by the line segments of the grid.
Q-6) Given n points on a circle \(A_1,A_2,..,A_n\), join the 2 points \(A_i\) & \(A_j\) to form the line segment \(A_iA_j\) for \(1\le i<j\le n\). Let \(S\) denote the set of all such line segments. Determine the maximum number of intersection points that can be formed by elements of \(S\).
Q-7) Define a sequence, where each term is either 0 or 1 by the term ‘binary sequence’. Let \(a_n\) denote the number of binary sequences of length \(n\) containing no 3 consecutive terms as \(0,1,0\) in that order. Denote by \(b_n\) the number of binary sequences of length \(n\) containing no 4 consecutive terms as \(0,0,1,1\) or \(1,1,0,0\) in that order. Show that \(b_{n+1}=2a_n\) for all positive integers \(n\).
Q-8) Let \(n\) be a positive integer greater than 1 and let \(T_n\) denote the number of non-empty subsets of \(\{1,2,3…,n\}\), such that the average of the subset is an integer. Show that \(T_n-n\) is even.
Q-9) Consider the regular octagon shown below:
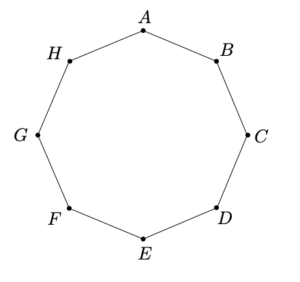
A frog starts jumping at vertex A, and from any vertex of the octagon except E, it can jump to one of its adjacent vertices. When it reaches E, it stops. Denote by \(u_n\) the number of paths of exactly n jumps ending at E. Show that
where \(x=2+\sqrt{2}\) and \(y=2-\sqrt{2}\) and \(n=1,2,3…\).
Q-10) Let \(S=\{1,2,3…,n\}\) and \(T\) be the set of all subsets of \(S\) (including \(S\) and the empty set). How many ways are there to choose 3 (not necessarily distinct) sets from \(T\) such that either 2 of the chosen sets are subsets of the third or one of the chosen set is a subset of both of the other 2 sets?