In general, locus of a complex number defines the path that the complex number can travel under certain constraints. Mathematically, it is the set of all points on the Argand Plane (also called the Gaussian Plane) that satisfy a given mathematical relationship. For example, let’s consider a simple equation : \(|z|=5\). What is the locus of \(z\)? So we are basically interested in the set of all points on the argand plane whose modulus is 5. As discussed in our first article on complex numbers, modulus represents the distance of a complex number from the origin or center of the complex plane. So this boils down to finding the set of all points, whose distance from the origin is 5 units.
Most of the problems on loci will be solved by sunstituting \(z=x+iy\) in the given equation. In this example, we intuitively feel that the set of all points which lie at a distance of 5 units froma fixed point will constitute a circle. Substituting \(z=x+iy\) and squarring both sides of that equation yields
\(x^2+y^2=25\)
Thus the set of all \((x,y) \in R\) satisfying \(x^2+y^2=25\) constitute the locus or path of \(z\).
What about \(|z-z_1|=5\)? More specifically what about \(|z-1-i|=5\)? The locus of all \(z\) satisfying this also constitutes a circle since we are interested in finding the set of all points which lie at a fixed distance (5) from a fixed complex (\(1+i\)).
So this boils down to \(|z-(1+i)|=5\). Substituting \(z=x+iy\) yields \((x-1)^2+(y-1)^2=25\). Intuitively, it should be easy to draw a referance to a complex number from a number represented on the 2D Cartesian Plane of real numbers. The complex vector \(\overrightarrow z = 1+i\), when thought from a 2D Cartesian concept is the line joining the origin and the point \((1,1)\).
What about \(|z-1-i|=|z-2|\)? Mathematically, the solution is to plugin \(z=x+iy\), followed by squaring of both the sides – which boils down to the simple relationship of a straight line \(y=x-1\). But let’s pause and think about this question :
Q) The locus of \(z\) satisfying \(|z-1+3i|=|z-6-9i|\) is :
a) Circle b) Straight Line c) A single point d) None of the above
We can definitely follow the approach, but a quicker (and far more elegant) method would be to analyze this and arrive at this conclusion :
The points which are always equidistant from 2 fixed points lie on the perpendicuar bisector of the straight line joining those two points.
How do we know this? Let’s go back to some ninth-grade mathematics.

Fig 1.1
Consider D to be the midpoint of BC. Let’s draw a perpendicular at D, and let A be any point on that perpendicular. It follows from elementary geometry that \(\triangle ADB \equiv \triangle ADC\). Thus, any point on the perpendicular at D, is equidistant from B & C. Thus if \(B = 1-3i\) & \(C=6+9i\), we have our locus as a straight line through their midpoint and perpendicular to the line joining BC.
Ex -1
Find the locus of \(z\) such that \(\frac{1+\overline{z}}{z} \in R\).
Solution:
One way is to substitute \(z=x+iy\), and then multiply both numerator and denominator by \(\overline{z} = x-iy\). Then equating the imaginary part to 0 will yield our locus.
The better solution would however use what we had learnt in our previous chapter and have
\(\frac{1+z}{\overline{z}} = \frac{1+\overline{z}}{z}\) \(\iff \overline{z} + \overline{z}^2 = z + z^2\) \(\iff (\overline{z} – z) + (\overline{z} – z)(\overline{z}+z) = 0\) \(\iff (\overline{z} – z)(1+\overline{z}+z) = 0\)We thus have one solution as \(z=\overline{z}\), which means \(z \in R\), but \(z \ne 0\). Another solution yields the line \(x = -\frac{1}{2}\). We must note that the property \(z = \overline{z} \iff z\in R \), even though trivial, comes in handy at times.
Ex – 2
Find the locus of \(z\) satisfying \(\left| \frac{3z+i}{2z+3+4i} \right| = \frac{3}{2}\)
Solution: Upon cross multiplication we have
\(\left| z+\frac{1}{3}i \right| = \left| z+ \frac{3}{2}+2i \right|\).
Note that we can represent this in the form \(|z-z_1|=|z-z_2|\), and thus the locus is the perpendicular bisector of the line joining the complex numbers \(-\frac{i}{3}\) & \(-\frac{3}{2} – 2i\).
Test Your Concepts:
Consider \(|z-z_1|=k|z-z_2|\). Does the locus of \(z\) depend on \(k\)? (Hint: What happens if \(k>1\))?
Some important points (We’ll cover these concepts in our Coordinate Geometry Module, but for now let’s note down these points)
- if the sum of the distances of a complex number \(z\)from 2 fixed points is always constant \(>|z_1-z_2|\), the locus of the complex number is an ellipse. In the following example the ellipse has 2 focii at \(z_1,z_2\). The distance between these 2 focii is \(ke\), where \(e\) is the eccentricity of the ellipse, and \(\frac{k}{2}\) is the length of the major axis.
In general, an ellipse has the equation \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\), and the eccentricity is given by the formulae \(e = \sqrt{1-\frac{b^2}{a^2}}\)
\(|z-z_1|+|z-z_2|=k\)(=constant \(>|z_1-z_2|\)). Here \(k=2a\), and \(a\) is the length of the major axis and \(b\) is the length of the minor axis. - if the absolute difference of the distances of a complex number \(z\) from 2 fixed points is a constant \(<|z_1-z_2|\), the locus of \(z\) is a hyperbola.
\(||z-z_1|-|z-z_2||=k\)(=constant \(<|z_1-z_2|\))
Ex-3:
Show that if \(P\) is a point on the circle with \(AB\) as diameter, where AB is a fixed line segment, then \(AP^2+PB^2\) is a constant
Solution:

Consider the above figure. Let E be the mid-point of AB. So E becomes the center of the circle, which means \(BE=PE\) & \(PE=AE\). Let \(\angle PBE = \alpha\). Since \(\triangle PBE\) is isosceles, we have \(\angle BPE = \angle PBE = \alpha\). Similarly if \(\angle PAE = \theta\), then \(\angle EPA = \theta\). We thus have \(2\alpha + 2\theta = \pi\). That implies \(\alpha + \theta = \frac{\pi}{2}\). Thus \(\triangle APB\) is a right angled triangle. And \(AP^2+PB^2 = AB^2\), which is a constant.
Thus the locus of a complex number \(z\) satisfying \(|z-z_1|^2+|z-z_2|^2 = k\)(=constant) is a circle.
Test Your Concepts:
Given AB is a fixed straight line, What will be the locus of point \(P\) such that \(\angle APB\) is always constant?
2.1 Triangle & Geometrical Properties
We have already discussed in the previous chapter that \(\overrightarrow{z_1}, \overrightarrow{z_2}\) constitute 2 sides of a triangle then the thrid side is represented by the vector sum of the other 2 sides. For any triangle, we know that the scalor sum of any 2 sides is always greater than the third side. So combining these we have what is popularly known as the Triangle Inequality
\(\fbox{$\displaystyle |z_1+z_2| \le |z_1|+|z_2|$}\).
We can also show that \(||z_1|-|z_2|| \le |z_1+z_2| \le |z_1+z_2|\). To prove the first inequality let’s consider the following figure

Fig 2.1.1
\(DH\) is the perpendicular on \(AC\) from \(D\). We thus have \(|z_1+z_2|^2 = |z_1|^2+|z_2|^2+2|z_1||z_2| \cos \theta \ge (|z_1|-|z_2|)^2\). Taking the positive square root of both the sides, we have our first inequality.
If \(z_1,z_2,z_3\) represent the three vertices of an equilateral triangle, we have
or
\(1\le i,j \le 3\)
Before we go into the proof , we need to get an important result : if \(|z_1|=|z_2|\) & \(arg(z_1)=arg(z_2)\), this implies \(z_1=z_2\). (Why?)
Since the three vertices represent an equilateral triangle \(|z_1-z_2|=|z_2-z_3|=|z_3-z_1|\). And we have \(\left| \frac{z_1-z_2}{z_3-z_2} \right| = \left| \frac{z_2-z_3}{z_1-z_3} \right|\). Also \(arg \left( \frac{z_1-z_2}{z_3-z_2} \right) = arg \left( \frac{z_2-z_3}{z_1-z_3} \right)\).
From these we have \(\frac{z_1-z_2}{z_3-z_2} = \frac{z_2-z_3}{z_1-z_3}\). From here it’s simple algebraic manipulation to yield the above equalities.
Test Your Concepts:
- When does equality hold for the triangle inequality?
- What is the locus of \(z\) satisfying \(|z-z_1|+|z-z_2|=|z_1-z_2|\)
- What is the locus of \(z\) satisfying \(|z-z_1|-|z-z_2|=|z_1-z_2|\)
- Show that \(|z_1-z_2| \ge ||z_1|-|z_2||\)
2.2 Addition of Complex Numbers – Geometrical Represnetation

Fig 2.2.1
Consider the above figure. Let D represent the sum of the complex numbers at C (\(z_1\)) and B(\(z_2\)). CD is the distance between complex numbers \(z_1+z_2\) & \(z_1\). Thus \(|CD| = |z_1+z_2-z_1| = |z_2| = |AB|\). Smilarly we have \(|AC|=|BD|\). Thus we have \(ABCD\) as a parallelogram, where D represents the complex sum of B & C.
We must note that that this result holds same for subtraction of 2 complex numbers as well. Gievn \(z\), we need to do 2 reflections to find \(-z\). (Remember that to find \(\overline{z}\) we needed just 1 reflection about the real axis). Reflect \(z\) about the real axis, and then do another reflection along the imaginary axis. The resultant point is \(-z\). And as should be obvious \(z_1-z_2=z_1+(-z_2)\), and thus we’ll still have the parallelogram property like we have discussed above.
2.3 Multiplication of Complex Numbers – Geometrical Representation
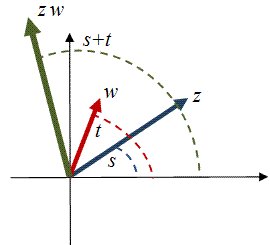 Fig 2.3.1
Fig 2.3.1
We have already shown in the first chapter using Euler’s formula and Demoivre’s Theorem how we arrive at the conclusion that a complex number is rotated in the anticlockwise direction, when it is multiplied by another complex number. Geometrically, it is as hown in the figure. One result to note is that
Thus \(\arg (zw) = \arg (z) + \arg (w) = s+t\). Also \(\arg \left( \frac{z_1}{z_2} \right) = \arg (z_1) – \arg (z_2)\). This comes from the fact that \(z=e^{i\theta } \iff z^{-1} = e^{i(- \theta )}\). Thus \(\arg \left( \frac{1}{z} \right) = -\arg (z)\). Thus in the case of division, the complex number is also rotated, but in the clockwise direction by the argument of the dividing complex number.
2.4 Coni’s Method
If \(A(z_1),B(z_2),C(z_3)\) form three vertices of a triangle defined in the counter clockwise sense, then Coni’s theorem states that
where \(\alpha = \angle BAC\). Note that if \(\alpha = \frac{\pi}{2}\) or \(\alpha = -\frac{\pi}{2}\), then \(\frac{z_1-z_3}{z_1-z_2}\) is completely imaginary.
<<In case there is any confusion over any example (solved or not), problem or concept, please feel free to create a thread in the appropriate forum. Our memebrs/experts will try their best to help solve the problem for you>>